Manifolds, Tangent Spaces, Cotangent Spaces, Submanifolds, Manifolds With Boundary 5.1 Charts and Manifolds In Chapter 1 we defined the notion of a manifold embed-ded in some ambient space, RN. In order to maximize the range of applications of the the-ory of manifolds it is necessary to generalize the concept. In particular, we still would like to "do calculus" on our manifold and have good notions of curves, tangent vectors, differential forms, etc. In Chapter 4 we defined the notion of a manifold embedded in some ambient space \ ( {\mathbb {R}}^N\). In order to maximize the range of applications of the theory of manifolds, it is necessary to.
What is a Manifold? Lesson 13 The tangent bundle an illustration. YouTube
Geometry of tangent vector field Download Scientific Diagram
Tangent spaces and Riemannian manifolds YouTube
A manifold M and its tangent space T p M at the point p. The geodesic... Download Scientific
This figure shows two points X and Y on a manifold M together with... Download Scientific Diagram
The tangent vector and space of manifold technique. Let ℂ denotes the... Download Scientific
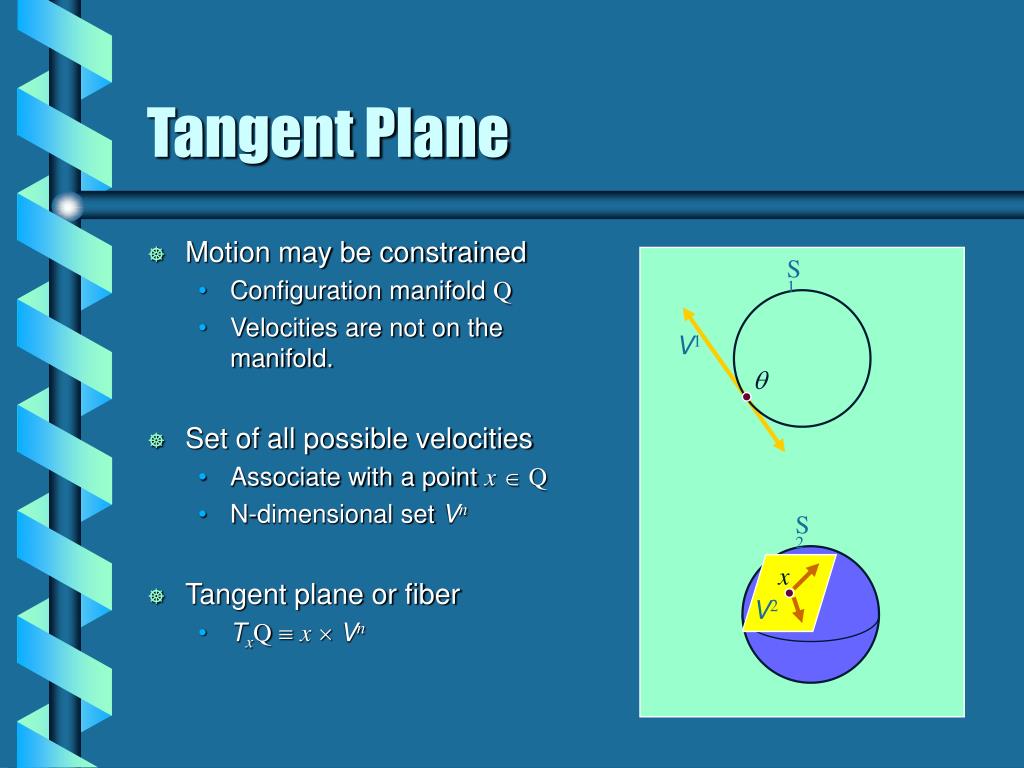
PPT Tangent Space PowerPoint Presentation, free download ID542442
What is a Manifold? Lesson 9 The Tangent SpaceDefinition YouTube
two dimensional shapes are shown in the diagram
Manifolds, Tangent Spaces, and Coordinate Basis Tensor Intuition YouTube
Tangent space of Stiefel manifold Download Scientific Diagram
A manifold, its tangent plane, and the correspondence between a line in... Download Scientific
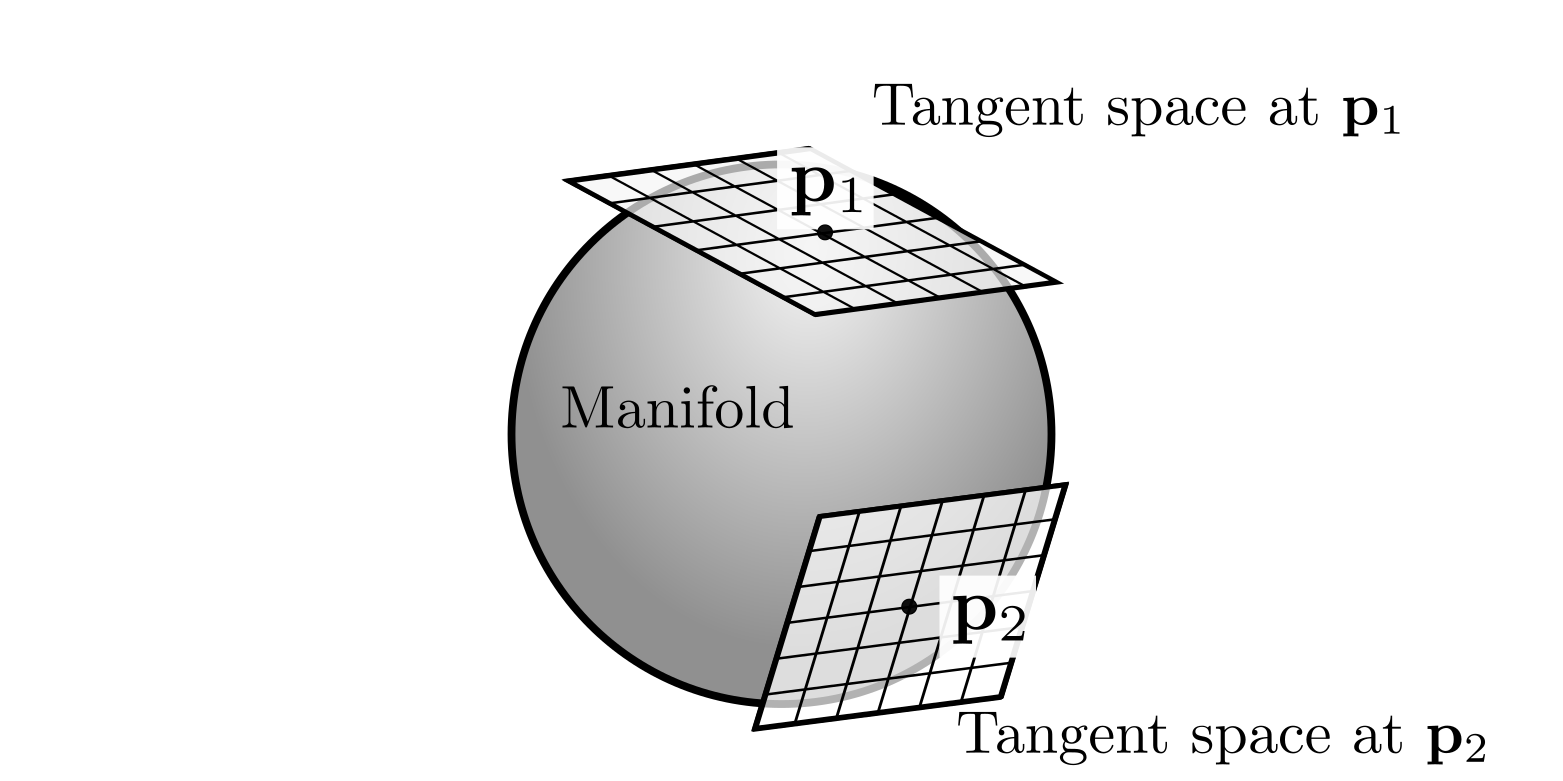
Reducing the uncertainty about the uncertainties, part 2 Frames and manifolds GTSAM
An embedded manifold M ⊂ E with its tangent spaces T (R) and a given... Download Scientific
Tangent space of Stiefel manifold Download Scientific Diagram
![Manifolds Part 19 Tangent Space for Submanifolds [dark version] YouTube](https://i.ytimg.com/vi/LEchROOY3pE/maxresdefault.jpg "Manifolds Part 19 Tangent Space for Submanifolds [dark version] YouTube")
Manifolds Part 19 Tangent Space for Submanifolds [dark version] YouTube
Illustration of basic geometric manifold concepts tangent vector space... Download Scientific
2manifold in 3space with normal and tangent vectors Download Scientific Diagram
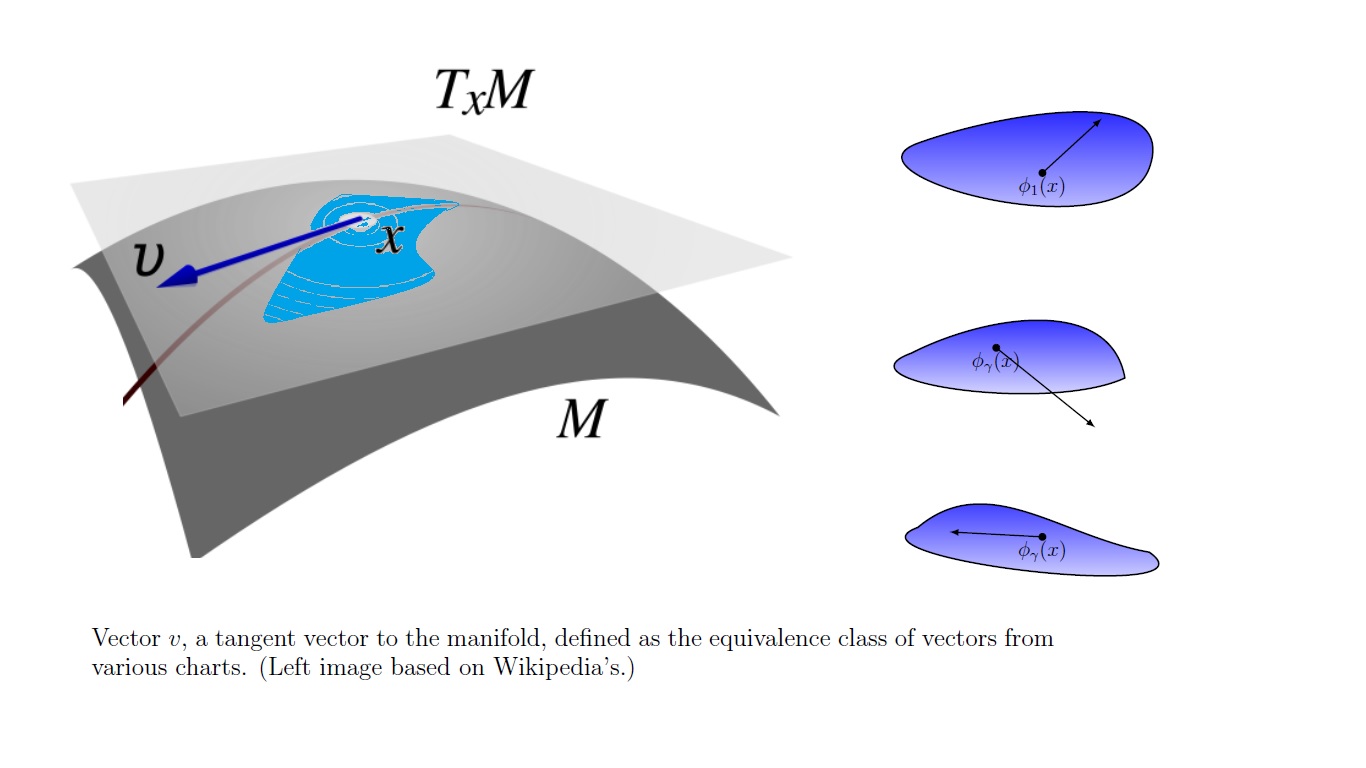
What Is A Manifold (6/6)
![[Solved] tangent space of manifold and Kernel 9to5Science](https://sgp1.digitaloceanspaces.com/ffh-space-01/9to5science/uploads/post/avatar/143236/template_tangent-space-of-manifold-and-kernel20220805-3225453-16i2iwg.jpg "[Solved] tangent space of manifold and Kernel 9to5Science")
[Solved] tangent space of manifold and Kernel 9to5Science
manifolds with boundary exactly as in the unbounded case, and we can also define a tangent space T(M) associated to a smooth manifold with boundary; over each point of M, including the boundary, one has an n - dimensional space of tangent vectors. At a point x on the boundary ∂∂∂M, the vector space Tx (M) contains a. In mathematics, the tangent space of a manifold is a generalization of tangent lines to curves in two-dimensional space and tangent planes to surfaces in three-dimensional space in higher dimensions. In the context of physics the tangent space to a manifold at a point can be viewed as the space of possible velocities for a particle moving on the manifold.
